1. What is the scheduling problem with energy storage?
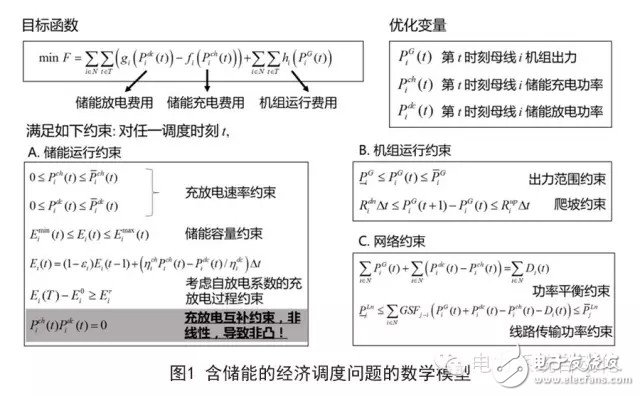
Energy storage plays a crucial role in modern smart grids, enabling more efficient and flexible power system operations. When integrated into economic dispatch, it helps reduce peak demand and accommodate renewable energy sources. The scheduling problem involving energy storage can typically be modeled mathematically, as shown in Figure 1 (assuming that the charge and discharge prices are given parameters). The goal is to minimize the total operating cost of the grid under various constraints, such as those related to energy storage operation, unit generation, and network limitations. With the inclusion of energy storage, two additional cost components must be considered: the cost of charging the storage and the cost of discharging it.When it comes to the charging cost, if the price is positive, it means the energy storage pays the grid for the electricity it takes in. Conversely, if the price is negative, the grid compensates the storage for the energy it receives. Similarly, for the discharge cost, a positive value indicates the grid pays the storage for the energy it releases, while a negative value means the storage has to pay the grid for the energy it gives back.
If there is a long-term contract between the energy storage system and the grid, the operational cost of the storage may not be directly included in the dispatch process. In this case, the charge and discharge prices can be set to zero, simplifying the model significantly.
2. What are the challenges of the energy storage scheduling problem?
Compared to traditional scheduling without energy storage, all energy storage-related problems face a fundamental challenge: an energy storage unit cannot charge and discharge simultaneously. This constraint must be incorporated into the optimization model. A common initial approach is to use a single variable representing the net power exchanged between the storage and the grid—positive when charging and negative when discharging. However, this method is not accurate because the efficiency of charging and discharging differs, and the associated costs vary depending on the time of day. Additionally, the financial flows differ based on whether the grid pays the storage or vice versa. Therefore, modeling this with just one continuous variable is insufficient. Instead, most studies use two separate variables—charging power and discharging power—to represent the storage’s behavior. This introduces complementary constraints, meaning at any given time, the product of the charging and discharging power must be zero. These nonlinear constraints make the optimization problem non-convex and difficult to solve efficiently.Although some methods attempt to simplify the problem by using penalty functions, smooth approximations, or discrete variables, they often require solving multiple sub-problems, which increases computational time and reduces efficiency. Hence, finding a way to handle these constraints effectively remains a key challenge in the field.
3. How to deal with this challenge? - The strict relaxation method
The main issue lies in the complementary constraint that prevents simultaneous charging and discharging. If this constraint were removed, the problem would become a standard convex optimization problem, which is much easier to solve. So, could we "ignore" this constraint during the solution process? That is, relax it in the model and see if the resulting optimal solution still naturally satisfies the original condition that the product of charging and discharging power equals zero? This article explores whether such a relaxation can be "strict" under certain conditions. If so, then in many practical cases, we could significantly simplify the optimization problem, improving both speed and efficiency.4. What conditions can make the relaxation "strict"?
Mathematical analysis shows that the relaxation is valid if two conditions are met simultaneously:Condition 1: For any energy storage, the discharge price must be greater than or equal to the charge price at all times.
Condition 2: For any energy storage, the charge price must be less than or equal to the node price at all times.
These conditions have clear physical and economic meanings. From an economic perspective, if both conditions hold, then simultaneous charging and discharging is not optimal. The optimal solution will naturally satisfy the complementary constraint without needing explicit enforcement.
5. How can we determine if these conditions are satisfied?
Condition 1 is relatively straightforward to check since the charge and discharge prices are inputs to the model. Condition 2, however, requires forecasting the node price over the scheduling period using historical data. If the predicted range of node prices ensures that the charging price is always below the lower bound of the node price, then Condition 2 is satisfied.6. Can these conditions generally hold in practice?
This depends on the market structure and pricing mechanisms in place. In many real-world scenarios, especially in regulated or well-designed markets, these conditions can be reasonably expected to hold. If they do, the relaxation method becomes a powerful tool for simplifying complex energy storage scheduling problems, leading to faster and more efficient solutions.12V Solar Charge Controller,60 Amp Power Solar Charging Controller,60A Solar Controller,Solar Charge Controller
GuangZhou HanFong New Energy Technology Co. , Ltd. , https://www.gzinverter.com